CPA FOUNDATION LEVEL CIFA FOUNDATION LEVEL QUANTITATIVE ANALYSIS
WEDNESDAY: 21 August 2024. Morning Paper. Time Allowed: 3 hours.
This paper has seven (7) questions. Answer any FIVE questions. ALL questions carry equal marks. Show ALL your workings. Do NOT write anything on this paper.
QUESTION ONE
(a) State FOUR characteristics of the mean as a measure of central tendancy. (4 marks)
(b) Describe FOUR assumptions of linear regression model as used in statistics. (4 marks)
(c) The total revenue function of producing product “G” is quadratic in nature. The following data shows the number of units of product G sold and the corresponding sales revenue in thousands of shillings:
Sales revenue (R) Sh.“000” 2,325 2,900 3,750
Number of units sold (Q)
Required: 15 20 30
(i) Formulate the total revenue function. (6 marks)
(ii) Determine the maximum revenue of producing product “G”. (4 marks)
(iii) Calculate the total revenue when the number of units sold is 80. (2 marks)
(Total: 20 marks)
QUESTION TWO
(a) In a classroom with 15 students, 4 of whom are girls, the teacher randomly selects 4 students for a group project.
Required:
Determine the probability that the group of the students selected will be composed of the following:
(i) 3 girls and 1 boy. (3 marks)
(ii) All boys. (3 marks)
(iii) At least one girl. (3 marks)
(b) The following frequency distribution table shows the amount of annual electricity bill obtained from a local utility company’s annual report:
| Electricity bill Sh. “000” | Frequency |
| 0 – 249 | 3 |
| 250 – 499 | 10 |
| 500 – 749 | 8 |
| 750 – 999 | 3 |
| 1,000 – 1,249 | 4 |
| 1,250 – 1,499 | 1 |
| 1,500 – 1,749 | 0 |
| 1,750 – 1,999 | 1 |
Required:
(i) Calculate the lower quartile and interpret your result. (3 marks)
(ii) Determine the median value of the electricity bill. (2 marks)
(iii) Compute the upper quartile value of the electricity bill. (2 marks)
(iv) Determine the quartile coefficient of skewness and interpret your result. (4 marks)
(Total: 20 marks)
QUESTION THREE
(a) An economy produces food, clothing and shelter. To produce one unit of food, it requires 0.6 units from food sector, 0.2 units from clothing sector and 0.1 units from the shelter sector. To produce one unit of clothing, it requires 0.1 units from the food sector, 0.4 units from clothing sector and 0.2 units from the shelter sector. To produce one unit of shelter it requires 0.1 units from the food sector, 0.4 units from the clothing sector and 0.4 units from the shelter sector.
Required:
(i) Determine the matrix of technical coefficient (A). (2 marks)
(ii) Compute the total output for food, clothing and shelter sectors to satisfy a final demand of 50 units of food, 400 units of clothing and 400 units of shelter.
Assume that;
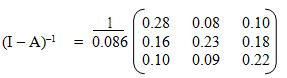
(iii) Account for the usage of clothing sector output determined in (a) (ii) above. (3 marks)
(b) Three judges rank 8 contestants in a talent show. The rankings assigned by each judge for all contestants are displayed in the table below:
| Contestant | A | B | C | D | E | F | G | H |
| Judge 1 Rankings | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Judge 2 Rankings | 2 | 1 | 3 | 4 | 6 | 5 | 7 | 8 |
| Judge 3 Rankings
|
1 | 3 | 2 | 5 | 4 | 6 | 7 | 8 |
Required:
(i) Using the Spearman’s rank correlation coefficient, determine the pair of judges that indicated the highest agreement in their rankings. (9 marks)
(ii) Describe TWO scenarios where one might prefer to use Spearman’s rank correlation instead of other correlation models. (2 marks)
(Total: 20 marks)
QUESTION FOUR
(a) The disease monitoring centre has established that the annual number of pandemic occurrence follows a Poisson distribution with a mean of 0.30 per annum.
Required:
(i) The probability that no pandemic will occur within a year. (3 marks)
(ii) The probability that at most two pandemics will occur within a year. (3 marks)
(b) Bobino Electricals Limited manufactures electric kettle and electric cookers.
Each electric kettle is sold at Sh.1,950 and each electric cooker is sold at Sh.2,400.
An electric kettle requires 3 kilograms of steel while an electronic cooker requires 5 kilograms of steel. Steel costs Sh.200 per kilogramme. It costs the company Sh.120 per hour to assemble each of the products.
It takes 5 hours to assemble an electric kettle and 7 hours to assemble an electronic cooker. There are 1,500 kilograms of steel available and a total of 2,450 hours available for assembling.
Required:
(i) Formulate the linear programming equations necessary to solve the above problem. (6 marks)
(ii) Solve the linear programming equations formulated in (b) (i) above graphically. (8 marks)
(Total: 20 marks)
QUESTION FIVE
(a) Describe TWO laws of probability. (4 marks)
(b) A company is contemplating an investment in either of the two machines; Machine A or Machine B to enhance its production capabilities. The decision requires assessing the costs and potential returns of each machine under varying market conditions.
The following information relates to the two machines:
Machine A
• Cost: Sh.100,000,000.
• Potential returns: Sh.250,000,000, if market demand is high and Sh.60,000,000 if market demand is low.
• Probability of high market demand is 0.70.
• Probability of low market demand is 0.30.
Machine B
• Cost: Sh.150,000,000.
• Potential returns: Sh.320,000,000 if market demand is high and Sh.80,000,000 if market demand is low.
• Probability of high market demand is 0.50.
• Probability of low market demand is 0.50.
Additionally, the company can choose to conduct a survey at a cost of Sh.20,000,000 to obtain more information before making the investment decision. The survey can indicate either favourable or unfavourable results with probabilities of 0.80 and 0.20 respectively, influencing the probabilities of market conditions.
If survey is favourable for both Machine A and Machine B:
• Probability of high market demand is 0.90.
• Probability of low market demand is 0.10.
If survey is unfavourable for both Machine A and Machine B:
• Probability of high market demand is 0.20.
• Probability of low market demand is 0.80.
The potential returns of Machine A and Machine B remain unchanged regardless of the survey outcome.
Required:
(i) Draw the decision tree for the above scenario. (10 marks)
(ii) Advise the management of the company on the best decision using the Expected Monetary Value (EMV) approach. (4 marks)
(iii) Determine the Expected Monetary Value from the decision made in (b) (ii) above. (2 marks)
(Total: 20 marks)
QUESTION SIX
(a) A random variable is normally distributed with a mean of 25 and a standard deviation of 5.
Required:
Using normal distribution approach:
(i) Calculate the value that will be exceeded 10% of the time assuming an observation is randomly selected from the distribution. (2 marks)
(ii) Compute the value that will be exceeded 85% of the time assuming an observation is randomly selected from the distribution. (2 marks)
(iii) Determine the two values of which the smaller value has 25% of the values below it and the larger value has 25% of the values above it. (2 marks)
(iv) Determine the value in which 15% of the observations will be below the distribution. (2 marks)
(b) A manufacturer claims that their packaging machine could fill a packet of sugar with an average weight of 600 grams.
A sample of 36 packets of sugar has an average weight of 500 grams with a standard deviation of 25 grams.
Required:
Test at a 5% significance level if there is sufficient evidence to reject the manufacturers claim. (6 marks)
(c) (i) Find the value of the following integral:
∫(4×3 + 2x + 5) dx for an interval between x = 1 and x = 3 (4 marks)
(ii) A function of a curve is given as:
Y = 3×2 – 12x + 64
Find the integral equation of the function. (2 marks)
(Total: 20 marks)
QUESTION SEVEN
(a) The data below represents the sales made by Yatta Traders for a period of three years:
Sales (Sh.“million”)
Quarters
Year 1 2 3 4
2021 4.4 10 15.8 6.4
2022 5.8 10.4 16.4 7.6
2023
Required: 6.4 11.6 18.2 8.2
(i) The 4-centered moving average trend values. (4 marks)
(ii) The seasonally adjusted additive indices. (6 marks)
(b) Highlight SIX assumptions of Markov analysis. (6 marks)
(c) Differentiate between “an interval estimate” and “a point estimate”. (4 marks)
(Total: 20 marks)